All-digits Arithmetic: Analysis Part 3

Mathematics is not about absolute, formulaic, only-one-way methods. It is about exploration.

We often forget to emphasize the creativity flowing through math, the skills of reading and understanding a question before setting out to solve it, and the continuous wondering and wandering involved as we solve it. We talk about these essential steps, but rarely model them. Or we model them occasionally in hopes our students know they should be applying these steps with every lesson, even if we don’t.

In the last two posts, we explored the determination of and connection between several distinct answers to an All-digits Arithmetic challenge posed in 2011 by Dennis Coble, a fellow tweeter and friend of mine.

Over the years several people have contributed to the solving of Coble’s challenge, including in the beginning, Ross Mannell, Earl Samuelson and Dennis himself. Others have further contributed to or used the problem, which led to me create the math lab associated with this challenge.

One of the more recent explorers and contributors has been Joe Lubich, a Google Plus and MeWe friend who I met in a Genetics and Evolution MOOC offered by Mohamed Noor.

Joe was the person who grouped the distinct answers into the nations and stabiles described at the end of the last post. He also investigated the extension of the challenge we will explore in this post.

Update: Actually, the extension will be explored in my next post. Here we will quickly explore how Joe worked through the All-digits Arithmetic challenge and the patterns he uncovered. This exploration is distinct enough from the extension Joe explored to warrant its own post. It also shortens the post into manageable pieces.

The following patterns make more sense after you read the first two posts analyzing this challenge.

Analyzing viable totals

Joe began solving the All-digits Arithmetic challenge by seeking answers that included two three-digit addends and a three-digit total. He found scattered answers, but he never knew how these answers related and whether more existed. So, a direct full-solution seems untenable.

When addition carried him only so far, he concentrated on finding viable totals (minuends for those exploring this challenge through subtraction).

He began by listing all the three-digit numbers from 000 to 999 in a 10 x 100 grid. He then circled the numbers with digital sums of 18; he actually hadn’t figured out that all correct totals had digital sums of 18 yet, but he noticed a pattern of correct answers (full additions) that highlighted these.

In his own words,

In an attempt at a new approach I listed all my [totals] in Excel and then sorted them from smallest to greatest. Then I found the difference between each [total] and the previous [total]. I was surprised to see that every difference was a multiple of 9, and then I noticed that every [total] was also a multiple of 9.

The three-digit numbers with digital sums of 18 line up in diagonals in nine-diagonal intervals.

Since all other numbers were distractions, Joe collapsed his sieve to include only those numbers he highlighted.

I skewed the resulting triangle to create this grid.

Notice, the original diagonals still line up in positively pitched inclinations.

To emphasize patterns, in this grid, I

• accented those totals containing the same digits with the same coloured background,
• included numbers, marked in red, which fit the grid, but are not viable totals,
• bracketed numbers with repeating digits and gave them grey fonts and white backgrounds, and
• (in the grids below) dropped 099, 909 and 990, since these had zero in them (and repeating digits).

Pattern: Viable-total symmetry

Glancing at the grid, you will notice a three-axis symmetry to it that divides the grid into six congruent, albeit chiral, parts. The axes of symmetry run through the numbers containing repeating digits (white backgrounds).

Notice the multi-way symmetry of the numbers in these six parts. Not only are the shapes of the parts congruent, so are the positioning of numbers with common digits.

This is emphasized in the following rendition of the grid.

In the grid above, the numbers are replaced by letters corresponding to the numbers’ background colours: L = blue, P = purple, R = red, Y = yellow, O = orange, B = brown and G = green. The mirror-symmetry of the grid parts and position-symmetry of numbers with common digits are much clearer. We not only see the radiant symmetries in this grid, the letters ripple out from the centre: L (blue 5,6,7) first to G (green 1,8,9) last.

The concentric arrangement of the numbers is a by-product of their radiant symmetry. A systematic repeat of numbers containing the same digits (L P R Y, L P R instead of L P R Y O B G) would warrant a deeper analysis. This is particularly true if the pattern were something like L P R Y R P L, a concentric symmetry. In both cases, exploring why the totals fall in this pattern and how the totals consequently relate would be fascinating.

Take a moment to appreciate the complex symmetries in this grid. Even though they suit the nature of the numbers, they continue to amaze me artistically and reveal depths I had not appreciated to the relationships of the viable totals.

The exchange of digits follows a pattern too, owing to the periodicity of the numbers, and reveals yet another symmetry. In each row, the first digit remains constant while the other two switch. In each positive diagonal, the mid digit stays the same. And in the negative diagonals, the last digit does not change. Further, the constant digits climb from 1 to 9 vertically and descend from 1 to 9 down each diagonal (corners are missing because the numbers that would occupy them — 909, 990 and 099 — have repeating nines and zero in them).

This produces a symmetry along the positive diagonals, where the mid digit is retained and the first and last digits switch. The first and last numbers of each diagonal reverse each other. So too the second and second last numbers, the third and third last, and so on to the middle of the diagonal, owing again to the constant periodicity of the numbers in the grid.

Pattern: Distinct-total symmetry

Lubich’s sieve contains 31 viable totals that resolve Coble’s challenge. Not all these sums are distinct as defined in my last post. Some of them are those variants where the free column, that neither lends nor borrows, is in the units place instead of the hundreds one.

This is the distribution of the distinct totals.

Notice here that the distinct totals tend toward the numbers, of greater value, to the upper right of the grid and are symmetrically grouped into nations.

• The a,b,c,l, g,h,i and d,e,f nations border the positive-diagonal axis of symmetry with each of a,c, b,l, g,i and d,f sharing the same totals mostly below the axis.
• u,t, n,m and k,j,q,s form three nations that hug the top and inclined-right edges of the grid. The answers associated with the first three pairs of totals are related by horizontal exchanges. The last, q,s, is rotationally related.
• o, p and r also share common digits. They are set in from the grid edges, rotational p and r beyond q and s and the main mass of distinct totals, o seemingly out of place, but symmetric with 684, which is not a viable total.

The totals with the floating free-digit (that neither lends nor borrows) in the units place have a similar distribution.

They tend toward the upper left of the grid, with “middle” number values, and are symmetrically flipped from the distinct totals.

No viable totals are found in the bottom centre of the grid, which contains numbers of lesser value. Also, as illustrated in the grid below, some distinct totals and free-units totals share common viable values.

It turns out the grouping of nations (via answer totals) is as interesting as the grouping of petals (via answer relationships). Since Joe followed his own solution to solving Coble’s challenge, the patterns unveiled by the nations illustrate more relationships among the totals of correct answers to the challenge than those explored in the last post.

It is possible to discover and explore these novel approaches and novel relationships because the All-digits Arithmetic challenge is an open exploration and not just another math exercise.

Which approach to solving Coble’s challenge did you find most enlightening? Please, comment and ask questions below. I look forward to seeing what you have to ask and say.

All-digits Arithmetic: Analysis Part 2

This is a long post. Take your time exploring it.

Last post we walked through a scheme to solve a math challenge posed by Dennis Coble, a fellow tweeter and friend of mine.

This challenge, which I dubbed All-digits Arithmetic, follows.

Here’s 1 that might interest you. Numbers 1-9 all used: 3 digit number, plus or minus 3 digit number, gives another 3 digit number.

Before moving further, I invite you to attempt to solve this challenge. I guarantee if you try it, it will engage you and get you thinking mathematically.

Spoiler alert: Reading further will spoil the fun and learning that attempting the challenge will provide. Try it before you read on.

 

Did you find all 336 answers to the challenge?

Congratulations if you did.

Today we are going to search for relationships between the 21 distinct answers to the challenge.

Before we do that though, we need to standardize what we define as a distinct answer. 

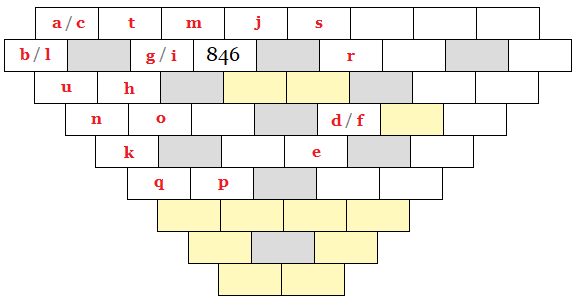
Defining a standard distinct answer

For each answer there are 16 variants.

These form a distinct family of answers — every variant is a sibling. So, there are 21 families with 16 siblings each.

For the moment, let’s label the siblings in the first row above 1 through 8 from left to right and repeat this labelling, using 9 through 16, in the second.

Now, we have all 336 answers and we want to intelligently talk about them, compare them and maybe even convert them into each other. So we pick variant 3 from family 12 and variant 7 from family 1 and compare them. We do the same to variant 14 from family 18 and variant 9 from family 20. (We can continue this way until all 336 answers are paired and compared.)

The problem we face, even if we find patterns, is that we cannot generalize from this hodgepodge of comparisons. The comparisons may not translate across all 21 families.

In order to intelligently communicate, compare and possibly convert the answers in a replicable way, we need to compare, say, variant 8 across all families. This means we need to decide on a standardized representative for each family.

This standardized representative will be the distinct answer and its siblings will be its variants.

You can pick any variant — variant 8 above, for instance — to be your standardized representative across families.

Defining distinct answers

Two parameters define each answer: the relative value of each digit in the same place-value position in the two addends and where the free column is.

This is my representative across the families. Again you can define yours as you like. Doing so might reveal different relationships between the families than I will describe here. This is why students should be set free to define their own representatives.

In my definition, the free column is in the hundreds place and each digit in the top addend is less than the digit below it in the bottom addend. There is nothing special about this definition; it is just what I chose so I can define what I am describing and comparing.

With this definition — with a definition — you are now able to understand what I am describing and replicate it if you wish. You can do the same with any other definition, so long as the definition is adhered to across families.

Okay, then. Enough of the terminology. You are here to learn how all these distinct answers relate.

But first another spoiler alert.

Stop: From this point I reveal the answers to the challenge. If you want to attempt the challenge, do not read further.

 

The distinct answers of Coble’s challenge

Here are my 21 distinct answers to Dennis Coble’s challenge.

Sort of anticlimatic given all the build-up, isn’t it?

For me though, this is the springboard for the fun stuff. The answers are just the start of the math.

Notice the free column is in the hundreds place in all my answers and each digit in the top addends has a value less than the digit in the same place in the bottom addends.

Also, I ordered and labelled these answers this way in light of the discussion that follows.

Analyzing the distinct answers

Finding the answers is a huge accomplishment. It requires systematic analysis or extensive brute force. But if we ended there, the All-digits Arithmetic challenge would just be another math problem, fun, full of learning and mathematical thinking, but no more than another exercise.

I never like to throw away an opportunity to explore. I have the answers. Now I want to know how they are related — if they are related, because math plays in connections, patterns and disruptions of these.

So, let’s do some exploring.

Inquiry: Vertical exchange of digits

We already described the vertical exchange of digits when we defined the 16 variants or siblings of each distinct family. What we found, for each answer, were these variants.

Notice all the vertical exchanges involve the addends only.

Applied to a specific family — here family ‘ l ‘, this familiar analysis produces the following pattern of answers. (Repeating this application across all 21 families produces a 21 x 16 grid.)

Attempting to exchange digits vertically across the sums, however, changes the digital sum of these totals, which breaks the observation proven last post that the digital sum of the total for each answer must be 18 for the answer to be correct.

A similar problem occurs when digits in the top addend and the sum are exchanged vertically. Notice above which answers don’t work and why.

Similarly, if you have been following along and you chose to explore subtraction instead of addition, any vertical exchanges that change the minuend break the answer and are not viable.

Math Lab 6 Question 4

With this inquiry and the standardization of the distinct answers, we resolve question 4 in the All-digits Arithmetic math lab.

4. Group all answers that can be converted into a distinct answer with that distinct answer. What manipulations of these answers will standardize the format of distinct answers?

Turning one distinct answer into another

The following analyses will resolve the next one.

5. What one-step manipulations will turn one distinct answer into another?

There are three types of transformation we can apply to our distinct answers to determine how they relate:

• digit exchange (vertical, described above; and horizontal, described below),
• digit rotation (90° CCW, 180° and 270° CCW), and
• digit flip (across the positive or primary diagonal and across the negative or secondary one).

To simplify the analyses, we will convert each distinct answer into a 3×3 grid in place of the addition or subtraction it now is.

Inquiry: Horizontal exchange of digits

Let’s continue comparing distinct answers by horizontally exchanging digits.

We can exchange digits horizontally simultaneously across one row, two rows or three rows.

When only one column is involved, no horizontal exchange is possible. Moving digits from one column must displace digits from another, which contradicts the one-column restriction.

On the other hand, there are 21 potential two-column horizontal exchanges. For example, given the digits abc, the exchanges are ab → ba, ac → ca and bc → cb. This pattern holds for each of the three rows individually, paired or grouped with the two other rows.

Notice for the two-column exchanges involving two rows, those rows can be contiguous (the two addends or the bottom addend and the total) or split (the top addend and the total).

Also notice that the exchange of the full middle column (b-e-h) with either edge column maintains the order of the other two columns. The two results place the middle column (b-e-h) to the far left or the far right of the other two columns, emulating the placement of the no-lending-nor-borrowing (free) column in the hundreds place and the units place of the challenge additions.

For horizontal exchanges involving all three columns, all digits in an exchanging row must move; otherwise, we have a two-column horizontal exchange. In the table above, digits in the first column move into the second, those in the second column move into the third and those in the third column move into the first. This pattern holds for each row, each row pair and for the full column of three rows.

For the digits abc in one row, the results of the three-column horizontal exchange are abc → cab → bca (→ abc). The right most column slides to the far left, emulating the movement of a free column from the units place to the hundreds place. Notice the Latin Square nature of the results.

Once again, the rows can be contiguous or split.

Further, like the two-column exchanges, there are 21 potential three-column exchanges.

Try finding those horizontal exchanges that relate distinct answers and convert the answers into each other.

Results: Horizontal exchange of digits

Twelve distinct answers relate pairwise through single horizontal exchanges.

Let’s describe the relationship of the a, b, c set of distinct answers. These distinct answers are interlinked to each other as follows.

Distinct answer a can be converted into b by horizontally exchanging the four digits in the bottom left corner. That is, digits 5 and 8 in the bottom of the free (left) column and digits 6 and 9 in the bottom of the borrowing (middle) column exchange, turning distinct answer a into distinct answer b.

a can also be converted into c with a similar exchange in the top left corner. So, 3 and 5 exchange with 2 and 6.

Meanwhile, b can be converted into c by horizontally exchanging the top left two digits, 3 and 2, and the bottom left two digits, 9 and 8, simultaneously.

These exchanges can occur in reverse as well. b can convert into a by horizontally exchanging the four digits in the bottom left corner of b, so creating a. (For now, don’t worry about the orange portion below.)

 

Imagine that: three distinct families interrelated to each other by one-step horizontal exchanges. Take a look at those distinct answers and see that 324, 657 and 891 repeat, interlinking the distinct answers like a chain, while 234, 567 and 981 do not. Also, in the top left corner of distinct answers a and c, the digits vertically add to eight in the middle (2 + 6 in a and 3 + 5 in c) and left (3 + 5 in a and 2 + 6 in c) columns.

This same set of exchanges also converts, and relates, distinct answers d, e and f, and g, h and i.

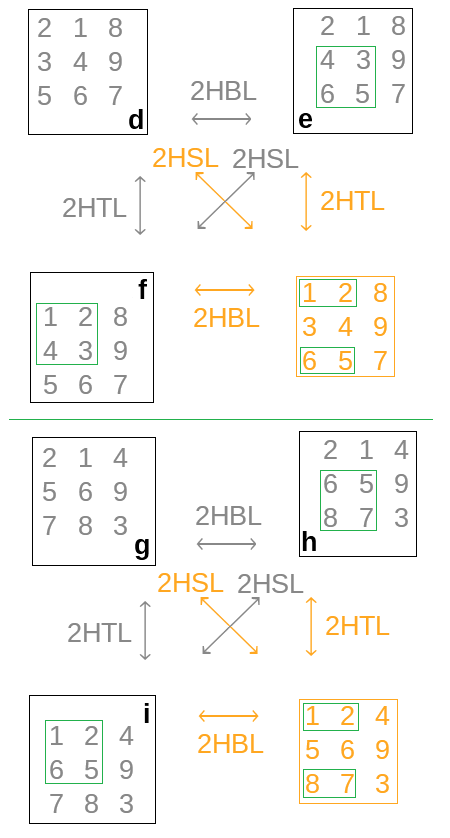
To simplify communication, I labelled the two-row horizontal exchange 2H; for one row, the horizontal exchange would be 1H, and for three rows, 3H. The top left corner is TL, the bottom left BL and the split left SL. (Right counterparts also exist. The group of four corner digits is labelled SS — split horizontally and vertically.)

The horizontal exchanges involving the nine distinct answers above follow this schema.

This schema illustrates that

• horizontally exchanging digits in the borrowing column and free column viably converts some distinct answers into others (the lending column is not involved),
• these exchanges are reversible (a converts to b iff b converts to a) and commutative (2HBL2HTL = 2HTL2HBL = 2HSL), and
• not all grids whose total or minuend rows have digital sums of 18 are answers nor even viable additions or subtractions (so the orange portion of the exchanges above).

Distinct answers j and k, and m and n, are similarly related except that horizontally exchanging the top left corners does not convert either distinct answer into viable additions nor answers. Because of this, neither 2HSL is viable either.

Why do j and k, and m and n not follow the same pattern as a, b and c, d, e and f, and g, h and i?

It is because the top left corner of each of j, k, m and n does not have digits that vertically add to the same total. For example, 2 + 4 = 6 in the left column of m, 1 + 7 = 8 in m‘s mid-column, 2 + 7 = 9 in n‘s left column and 1 + 4 = 5 in the mid-column of n.

The 2HTL exchange only works if the four digits being horizontally exchanged add vertically to the same sum. The schema that worked so well for the first nine horizontal exchanges above must be modified to account for this restriction.

With this modification, eleven of the twelve horizontal-exchange relationships can be explained by this schema.

Finally, t and u are related through a 2HSL exchange. Neither the 2HTL nor 2HBL exchanges in the modified schema produce viable additions here.

or

2HTL exchanges do not work for t and u for the same reason they do not work for j and k, and m and n.

I don’t know why the 2HBL exchanges do not convert t and u into viable additions, beyond the fact that the additions do not work. Perhaps this is an investigation you might pursue. Or a more fruitful pursuit may be to ask why 2HBL works for all the other conversions involving 2HBL.

u was the last distinct answer I found and I found it because of this exchange.

Inquiry: Rotation of digits

Well, that was rather informative. We found twelve related relationships between distinct answers and a new distinct answer. Let’s try another transformation: rotation of digits.

Since each answer is an orthogonal grid and remains so, we have three possible rotations to deal with. A 90° turn rotates digits 90° counterclockwise; the block of digits that rotates flops onto its left side. A 270° turn on the other hand rotates the digits 90° clockwise — a flop to the right. Finally, a 180° turn rotates them 180° — on the block’s head. This is actually my favourite rotation because it is equivalent to a flip across the positive diagonal of the block, then another across the negative diagonal, or a horizontal exchange of the block digits, then a vertical one.

The following rotations then are possible.

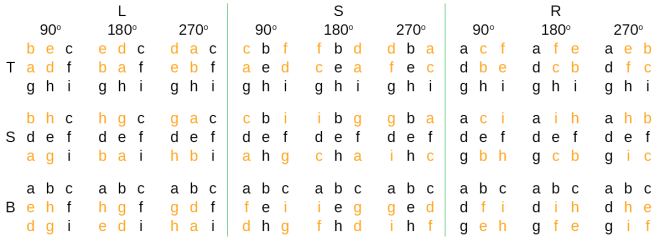
Before we continue, determine on your own what rotations relate distinct answers.

Results: Rotation of digits

Only the 180° rotations connect distinct answers in one step.

Distinct answers a, c; d, f; and g, i are related by a 2HTL exchange. They are also related by a 180TL rotation, after the rotation is standardized (a < d and b < e). (Why does this make sense?)

Notice that only the addends in the free and borrowing columns are involved in these rotations. These are also the digits that, in each pair of distinct answers, add vertically to the same sum.

Let’s try something else. Rotating d by 180BR produces j after standardization, while rotating it by 180BS produces n. These same rotations convert e into m and k respectively.

As illustrated in the diagram above, d and e, j and k, and m and n themselves are related by 2HBL exchanges: 3 and 5 switch with 4 and 6 (in d and e), 3 and 5 switch with 7 and 9 (in j and k), and 4 and 6 switch with 7 and 9 (in m and n). Note the chain-linking of these distinct answers reminiscent of similar linking of a, b and c; d, e and f; and g, h and i.

Obviously, j and m, and k and n are also related through these relationships.

Finally, p and q are related by a 180BS rotation, while r and s are related by a 180BR one, both sans standardization.

This makes nine one-step rotation conversions. But there’s more. 

Aside: A special two-step conversion

The conversion of p into r and q into s is 90TL1HBL. From there a simple r, s conversion converts p into s and q into r. If you look closely p also converts into s and q also converts into r by starting with a p, q conversion, then applying 90TL1HBL.

The reverse conversion, turning r into p and s into q, is 1HBL270TL or 270TL1HBL. 90° clockwise is the reverse of 90° counterclockwise. Preceding that with a simple r, s conversion, or following it with a p, q conversion, converts r into q and s into p.

Notice only the free and borrowing columns are involved in the two-step conversion. The lending column is not, again.

Inquiry: Flipping of digits

The horizontal and vertical exchanges are really reflections across the vertical and horizontal axes. Flipping is a reflection across a diagonal, either the primary or positive one (F1) or the secondary or negative one (F2).

There are 18 potential flip transformations.

Try to find flip transformations that relate distinct answers.

Results: Flipping of digits

Did you figure it out? There are no one-step flips that convert one distinct answer into another.

But there are two-step ones.

j converts into m using F2SSF1BS; k into n uses F2SRF1BR. The reverse conversions, turning m into j and n into k, use the same formulae. The details parallel those of converting p and r, and q and s.

What about 3-Row and 3-Column transformations?

Except for the horizontal movement of the free column from the units place to the hundreds place and vice versa, and the vertical exchange of the addends, there are no viable 3-Row and 3-Column transformations that change one answer into another.

Summary: Relating Distinct Answers

Our analyses revealed 37 conversions connect answers in the All-digits Arithmetic challenge.

1. Free = 2 — the free column (that neither lends nor borrows) can float between the hundreds place and the units place.
2. V = 8 — the digits in the addends are vertically commutative; with two addends and three digits, that makes 8 vertical exchanges.

The above two parameters group answers into 21 distinct families with each answer being a sibling — Siblings = 16.

3. H = 12 — (all 2H) two rows exchange digits horizontally in the following ways:
• a,b,c, d,e,f and g,h,i are related by 2HTL, 2HBL and 2HSL,
• j,k and m,n are related by 2HBL (2HTL does not work because the addend digits involved add vertically to different sums), and
• t,u is related by 2HSL.
4. R = 9 — (all 180°) four digits rotate in the following ways:
• a,c, d,f and g,i are related by 180TL (this is related to the 2HTL exchange and the digits’ common vertical sums),
• p,q, d,n and e,k are related by 180BS, and
• r,s, d,j and e,m are related by 180BR.
5. F = 0 — there are no one-step flips of digits that relate distinct answers.
6. l and o = 0 relationships — these two distinct families do not relate to any others, including each other.

The 2HTL exchange and 180TL rotation of a,c, d,f and g,i illustrate that some distinct answers can be converted into each other in more than one way.

Most conversions involving more than one step are forced and non-generalizable at best. There are a few though that systematically convert distinct answers in relatable ways.

1. p,r and q,s are related by 90TL1HBL, and open the way to relate p,s by 90TL1HBL180BR (pr,rs) or 180BS90TL1HBL (pq,qs) and q,r by 90TL1HBL180BR (qs,sr) or 180BS90TL1HBL (qp,pr). Notice these last four are the same two conversions, showing that conversions relate more than one pair of distinct answers, depending on the starting answer.
2. j,m is related by F2SSF1BS, and opens the way to relate j,n by 180BR180BS (jd,dn), F2SSF1BS2HBL (jm,mn) and 2HBLF2SSF1BS (jk,kn). Again, there are just two conversions here (transformations are commutative).
3. k,n is related by F2SRF1BR, and opens the way to relate k,m by 180BS180BR (ke,em), F2SRF1BR2HBL (kn,nm) and 2HBLF2SRF1BR (kj,jm). Notice the parallel to the conversions of j,m and j,n.

Pattern: Relationships between transformations

180° and 2H are related, after addend standardization (a < d, b < e and c < f), except when the total (bottom) or minuend (top) is involved. So are 90° and F2, and 270° and F1 under the same conditions.

Compare the shaded grids below. We are using distinct answer a as an example.

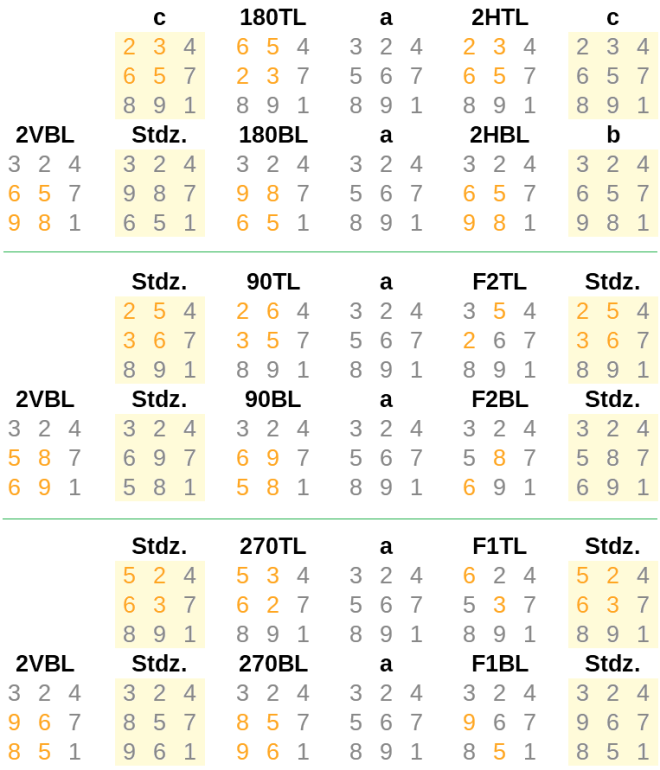
Notice that adding 2VBL — vertically exchanging digits in the bottom rows of the free and borrowing columns — resolves the discrepency between the shaded grids when the total is involved in the conversion. (Why does this work?)

Notice also that most of these grids are not correct additions. Here we are treating the digits as entries in grids, not as digits in numbers.

To see this point for yourself, try the above conversions with distinct answer o: 125 + 739 = 864. We know for o none of the additions will be correct (they would relate o to other distinct answers otherwise), so we can concentrate on the grid of digits.

Pattern: Families, clans, sets, petals and kin

One thing that the above analyses have shown us is that the answers to Coble’s challenge are related at several scales.

Following is a summary of these scales.

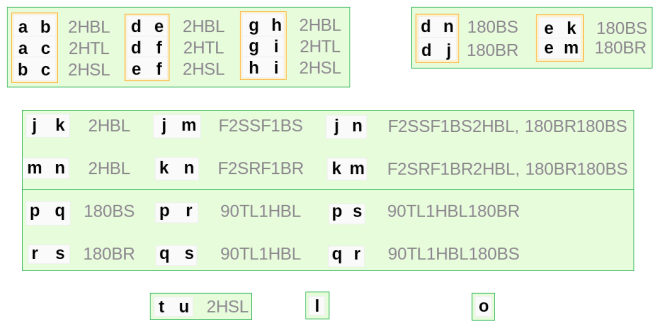
1. 21 families — Each bold letter corresponds to a distinct answer, which represents a family of 16 siblings.
2. 20 clans — Each grey box corresponds to a relationship or conversion. The pair of letters in this box form a clan, two families linked by a direct (one-step) connection. The two- and three-step conversions are extensions and not separate clans. l and o are placed in (pseudo-)clans containing only one family.
3. 5 sets, or camps — When these clans are connected by interlinked distinct answers and conversions, they form a set (orange).
4. 7 kin — Clans with similar conversions are grouped into a box of kin (green).
5. Kin with parallel conversions are stacked on each other; they share a common border.
6. 14 petals — Stacked and lone clans also form petals. These are the grouping of clans as described in this post: a,b,c; d,e,f; g,h,i; j,k; m,n; t,u; p,q; d,n; e,k; r,s; d,j; e,m; l; and o. They will be summarized in the following section.

This analysis resolves the last question in the All-digits Arithmetic math lab.

6. Group distinct answers, that can turn into each other in one step, into clans. How many clans are there? Are these one-step manipulations unique in each clan?

Pattern: All-digits Arithmetic flower

The distinct answers are arranged here in petals, nations and stabiles. Click on the flower to enlarge it.

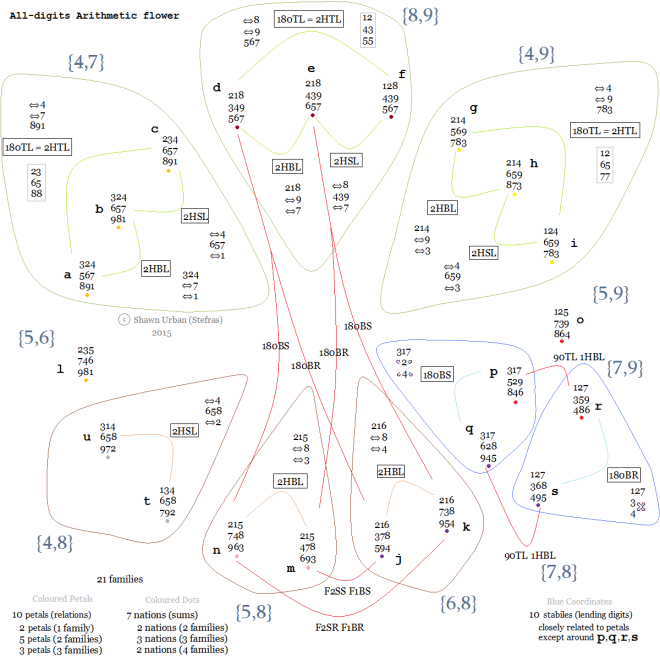
Notice the three sets a,b,c; d,e,f and g,h,i form three radiating petals as do j,k; m,n and t,u. p,q and r,s, meanwhile, form two “tangential” petals. And finally l and o form a petal each (not drawn). d,j; d,n; e,k and e,m do not form petals as such, but their conversions are drawn through the centre of the flower. These petals reflect relationships between the distinct families.

The petals are ordered so those distinct answers with the same digits in their totals are grouped into nations. So, a, b, c and l with digits 1,8,9 in their totals are grouped together. d, e and f have digits 5,6,7. g, h and i have 3,7,8. o, p and r have 4,6,8. j, k, q and s have 4,5,9. m and n 3,6,9. And t and u 2,7,9.

The stabiles are nearly identical in arrangement to the petals, except that p and r, and q and s are grouped together instead of p and q, and r and s. This is why the petals formed from these four families are tangential rather than radial. Stabiles reflect the immutable addend digits in the lending column. {4,7}, for instance, are the addend digits in the lending columns of a, b and c.

Joe Lubich, who you will hear more about next post, is responsible for the nation and stabile groupings.

Next post

Next post we will explore some extensions to the three-digit three-number All-digits Arithmetic challenge.

Did you like these analyses? Did you discover some new math? Please, comment and ask questions below. I look forward to seeing what you have to ask and say.

All-digits Arithmetic: Analysis Part 1

In my last post, I reposted a challenge proposed by Dennis Coble. In this post, I begin analyzing it. The two posts start the same to catch people up. Grab a pencil, eraser and paper, because it’s about to get mathematical.

Back in June 2011, friend and fellow tweeter, Dennis Coble, tweeted a math challenge to me. I posted this challenge, which I called All-digits Arithmetic, on my blog.

The challenge was so popular, three years later, I created a math lab of the same name based on it. And over the years several teachers and math recreationists have attempted Dennis’s challenge and contacted me about it and my math lab.

I use it myself when I need a filler for math classes I sub and for those math students who are done everything. It is one of those simple recreations that keeps students engaged and thinking mathematically. To date, no student I have subbed has found an answer to this math challenge, even when he or she has an entire period or even a block (two periods) to work on it.

Today and for the next two posts, I want to analyze this challenge.

But first let me repost it.

Math Challenge: All-digit Arithmetic

Here’s 1 that might interest you. Numbers 1-9 all used: 3 digit number, plus or minus 3 digit number, gives another 3 digit number.

Some clarification of the challenge might help. Every answer to the challenge contains two addends and a total; or a minuend, a subtrahend and a difference. That is, every answer contains three numbers that each contains three digits.

Also each digit from one to nine is used, once — no repeats in the entire answer. Several people approach me with additions or subtractions that involve three three-digit numbers (yea!), but that also repeat a digit, say 2, in one of the addends and the total, or in the minuend or subtrahend and the difference. These additions and subtractions violate the rules of the challenge. No digits repeat anywhere in legitimate answers.

With that, I invite you to attempt the challenge.

Analyzing the Challenge

Okay, ready?

Spoiler alert: The following analyses have solutions to this challenge. Reading further will spoil the fun and learning that attempting the challenge will provide. Don’t give up. There are answers — 336 of them to be exact.

 

I will break this analysis into three parts. Today, I want to explore the construction of answers to the challenge. In my next post, I want to explore relationships between the answers. And in the third, I want to explore extensions to it.

I will start with the construction of answers to the challenge. This post will cover questions 1 – 3 in the math lab, except I will not list the distinct answers.

1. How many answers are there? Assume one operation: either subtraction or addition.
2. What underlying patterns exist in these answers, such that the minuend or total does not change? What can be changed? What must stay unchanged?
3. How many distinct answers are there? List them.

Defining the form of answer to find

Answers involving the same three numbers can take four forms: two additions and two subtractions.

abc + def = ghi,
def + abc = ghi,

ghi − abc = def, and
ghi − def = abc.

Each of these equivalent forms can be a legitimate answer, but analyzing them all would double our work; we would literally repeat the same work twice without advancing the search for answers to the challenge. So we must pick a form to analyze.

I pick abc + def = ghi. You might pick one of the others. Choose one that makes sense to you.

Pattern: Exchanging addend digits vertically will not change the sum

Addends are commutative. But, so are the digits with the same place value in these addends.

This leads to eight correct variants for every distinct answer: two addends means for each place value two permutations are possible, and with three digits, three place values can be switched.

The equivalent pattern for subtraction is to exchange subtrahend and difference digits vertically without changing the minuends.

Whatever number of distinct answers there is, we now know it is at least one eighth the number of answers.

Pattern: Borrowing may be necessary

Adding all possible pairs of digits from 1 to 9 produces an addition table.

For this addition table, we are only interested in the values of the units (right-most or ones-place), since only these may appear in the challenge answers.

The diagonal of 10s is ignored since no zeros are allowed in the answers. The shaded diagonal with even values 2 through 18 is ignored since the values in this diagonal are sums of a digit added to itself (no repeats).

This leaves two triangles (white) with values 3 to 9 and 11 to 17.

The 11 to 17 triangle suggests that some lending and borrowing might be part of the solution to the challenge. In particular, values in this triangle lend 1 to the place value directly left of it, leaving unit values 1 through 7 to be included in the answer.

To see what is happening more clearly, the following table blows apart the addition table into lending, borrowing and free (neither borrowing nor lending) sections.

Once again, shaded addends are ignored, most because they repeat a digit. However, those necessarily involving 0 or 10 are also shaded, since zeros in the units-place are disallowed.

In their turn, sums with no viable addends are ignored (shaded) too.

Notice, the only viable digits in any lending-sum are 1 through 7, those in any borrowing-sum are 4 through 9, and those in any free-sum are 3 through 9.

Notice also, where two digits add to a double-digit number, lending must occur and the borrowing column must be immediately left of the lending column, as is standard in mathematics.

On the other hand, any column that neither lends nor borrows is free to float to the left or right of the lending-borrowing block.

This means, for each distinct answer to the challenge, there may now be 16 variants.

I will leave it to you to determine if lending and borrowing is in fact necessary and if it can occur twice in the same answer. (Hint: Think parity.) 

Pattern: Digital sum of the total is 18 in every answer

The digital sum of a number is the sum of its digits. So, the digital sum of 876 is 8 + 7 + 6 = 21. 876 also has a digital root, which is the iterative addition of it digits until only one digit, the number’s digital root, remains. For 876, 8 + 7 + 6 = 21, and 2 + 1 = 3, the digital root of 876.

I claim the digital sum of the totals of all legitimate answers to the challenge is 18.

This proof follows Task 43: Number Tiles.

Stop: From this point actual values are used. If you want to attempt the challenge, do not read further.

 

Okay, we’re back.

Let’s try to determine how many distinct three-digit sums have digital sums of 18. We can use a sieve-like analysis to narrow the number of possibilities from the blown-apart table.

Greyed combinations are repeats. Note, for the cases containing 7 in the sum, 4 + 7 + 7 = 18 is missing because 7 is repeated. For the same reason 2 + 8 + 8 = 18 is missing.

This gives 42 possible distinct sums: seven combinations × six permutations each. Not bad for a little analysis.

The digits of the addends associated with these sums follow.

That ends the search for answers to the All-digits Arithmetic challenge, other than to actually determine the answers.

We started with a huge though simple problem and systematically narrowed the possible answers to a reasonable few.

So, how did we do?

How many answers are there to the challenge?

1) In every answer, each of the digits 1 – 9 is used, each once only.

After choosing a digit to enter into the puzzle, eight digits are left for the second selection, then seven, six, and so on. The number of possible answers to the challenge at the onset is then

9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 9! = 362 880 possible answers.

2) For each distinct answer there are 8 permutations of the addends.

This reduces the number of possible distinct answers to an eighth of the onset number.

362 880 ÷ 8 = 45 360 possible distinct answers.

3) One column of digits, which neither lends nor borrows values, can float between the units and hundreds places. (You did confirm that the free-borrowing-lending structure is necessary, right?)

This halves the number of possible distinct answers.

45 360 ÷ 2 = 22 680 possible distinct answers.

4) However, from the blown-apart addition table, we know only some digit combinations fit the free-borrowing-lending structure.

Brute analysis of the table (which I will leave to you), and removal of sums with repeating digits, reduces the number of possible distinct answers to a whopping 192. Whoop!

Can we do better?

5) The digital sum of all correct totals is 18.

This reduces the number of possible distinct answers to 24 (after the reduction due to the free-borrowing-lending structure), a subset of the 42 possibilities from the permutation table after the sieve analysis.

6) These are few enough to conduct brute force mechanical solving, which reveals 17 actual distinct sums.

7) However, it also shows some sums are repeated in different distinct answers. Despite the fact the same digits are used in the addends, the digits are mixed horizontally, making distinct addends totalling to the same sum. Since the addends are distinct, so are the answers.

The horizontal mixing of digits here is separate from the floating of the free column that neither lends nor borrows.

This increases the number of distinct answers to 21.

With the 16 variations of each distinct answer, we get 336 answers to the challenge, certainly enough for some students to find one or two of them.

With the information above, you should be able to solve the challenge and find all 336 answers.

So, what’s next?

Next post, we will search for relationships between the 21 distinct answers. The post following, we will explore some extensions to the challenge.

But before I post that, I invite you to analyze how the distinct answers are related yourself. To me, this is where the fun begins.

This exploration of how the distinct answers are related addresses questions 4 – 6 of the math lab.

4. Group all answers that can be converted into a distinct answer with that distinct answer. What manipulations of these answers will standardize the format of distinct answers?
5. What one-step manipulations will turn one distinct answer into another?
6. Group distinct answers, that can turn into each other in one step, into clans. How many clans are there? Are these one-step manipulations unique in each clan?

Did you like this challenge? Did you like this analysis? Please, comment and ask questions below. I look forward to seeing what you have to ask and say.

All-digits Arithmetic: Renewing the Challenge

Back in June 2011, friend and fellow tweeter, Dennis Coble, tweeted a math challenge to me. I posted this challenge, which I called All-digits Arithmetic, on my blog.

The challenge was so popular, three years later, I created a math lab of the same name based on it. And over the years several teachers and math recreationists have attempted Dennis’s challenge and contacted me about it and my math lab.

I use it myself when I need a filler for math classes I sub and for those math students who are done everything. It is one of those simple recreations that keeps students engaged and thinking mathematically. To date, no student I have subbed has found an answer to this math challenge, even when he or she has an entire period or even a block (two periods) to work on it.

I have been asked several times to post a solution to the challenge. After eight years, I’ve decided to cave. Eight years is long enough to solve the problem, right?

In the next three posts, I want to analyze this challenge.

But first let me repost it.

Math Challenge: All-digit Arithmetic

Here’s 1 that might interest you. Numbers 1-9 all used: 3 digit number, plus or minus 3 digit number, gives another 3 digit number.

Some clarification of the challenge might help. Every answer to the challenge contains two addends and a total; or a minuend, a subtrahend and a difference. That is, every answer contains three numbers that each contains three digits.

Also each digit from one to nine is used, once — no repeats in the entire answer. Several people approach me with additions or subtractions that involve three three-digit numbers (yea!), but that also repeat a digit, say 2, in one of the addends and the total, or in the minuend or subtrahend and the difference. These additions and subtractions violate the rules of the challenge. No digits repeat anywhere in legitimate answers.

With that, I invite you to attempt the challenge.

And next week, I will post the first part of my analysis. It will given you hints you can pursue, almost right to the answer, but not the solution. The answer will come in two weeks, when the math gets really fun.

So, are you ready? Can you solve Coble’s Challenge and unravel the All-digits Arithmetic? Comment below and let’s see how you do.

Math Challenge: Can You Draw This?

picture perfect patch © 2011 randomtruth | more info (via: FlickrStorm)

 

Please, do not visit her post just yet

Fawn Nguyen wrote a post on Friday that caught my attention.

She divided her math class into pairs, making one person in each pair a Describer and the other person a Drawer.

She then gave the Describers a figure the Drawers were supposed to draw at 1:1 scale and three rules designed to prevent the Drawers from seeing the figure, the Describers from seeing the Drawers’ drawings, and either from using gestures and body language to signal information.

They were allowed to talk all they wanted.

I thought today I would be your Desciber. We can use the comments to this post to talk to each other.

Exercise in visualization and communication

This Challenge is an exercise of visualization, communication and knowledge. Visualizing and knowing what one is seeing (recognition: visualization, knowledge); describing this efficiently and effectively (oral communication); visualizing what is described (listening, visualization); connecting that visual to known shapes and images (knowledge); and efficiently and effectively drawing the visualized figure to scale (visual and haptic communication, knowledge) are foundational skills our students need to use and communicate mathematics both within and beyond the classroom.

I participated in a similar exercise Dr. David Pimm conducted in a Math ed graduate class. The Describer picked a part of a much larger and more complex figure than Nguyen’s figure and described it and its location to the Drawer. The Drawer visualized, located and identified, rather than drew, what the Describer was seeing. We were required to sit on our hands, a behaviour that would have made Nguyen’s Drawers’ jobs much harder. But the Describer and Drawer in Pimm’s class had to confirm orally that the visualizations match (secret messages, discrete mathematics), a slightly different skill than Nguyen’s Drawers were learning.

Both exercises are simultaneously frustrating and engaging, like an addictive game one struggles in, cannot win and yet cannot put down. By design, the exercises target these emotions; one’s communication and visualization skills; and one’s knowledge. These are emotions and skills that a majority of their time the mathematician and the teacher — indeed all people — encounter and need to cope with. (For this reason, Pimm’s exercise was perfect for preservice teachers.)

 

Garry Oak Ecosystem in a Dewdrop © 2007 Evan Leeson | more info (via: FlickrStorm)

 

Good luck. Enjoy this math Challenge.

Ready, set, …

There is only one rule here: do not visit Nguyen’s post no matter how tempted you are to do so until you have finished drawing your figure.

Feel welcome to comment me with queries, comments, your final drawing, instructions for a figure you find or design (please provide a URL to this figure, so others and I can find it, and yet not see it here), and most importantly your reflections (both experiential and critical) after taking up this challenge.

Draw a figure following these instructions.

1. Use a ruler and a compass to draw this figure. Blank paper; a sharp pencil (2H or harder); eraser; and either coloured pencils (green, light blue and dark blue), another sharp pencil (HB or softer) or a pen (or three of different colours) may also help.

 

2. With a sharp hard pencil (2H or harder), lightly

1. construct three concentric circles with radii of 32 mm, 59 mm, and 78 mm.
2. draw a diameter across the smaller, inner (32 mm) circle that also intersects the larger, outer (78 mm) circle twice, with ticks.

 

3. poke your compass into one of the intersections of the inner circle and its diameter;
4. without lifting the poked end of your compass, stretch your compass to the opposite arc of the middle (59 mm) circle; and
5. scratch an arc above and below (orthogonal to the diameter) the common centre of the concentric circles.
6. repeat the last two instructions after poking the other intersection of the inner circle and its diameter.
7. use your ruler to “connect” each intersection of the arcs and the common centre of the circles.
8. with your ruler set as just instructed, draw a diameter across the inner circle and two ticks intersecting the outer circle.

 

Notice, the two diagonals now frame four 90° angles.

 

9. poke your compass back into one of the two holes that you just made in the inner circle.
10. scratch an arc across the middle of the two 90° angles adjacent to the diameter you are “in”.
11. repeat the last two instructions for each of the remaining three intersections of the inner circle and its two diameters.
12. use your ruler to “connect” the intersections of opposite arcs and the common centre of the circles.
13. with your ruler set as just instructed, draw a diameter across the inner circle and two ticks intersecting the outer circle.
14. repeat for the other pair of opposite arcs.

 

There are now four diagonals that frame eight 45° angles.

 

15. once again create arcs to bisect these angles following instructions 2i — 2l.
16. for each pair of opposite angles, with your ruler set as instructed, scratch a tick where the ruler intersects the middle circle (eight ticks total).

 

17. starting with one tick intersecting the outer circle, connect that point of intersection with an adjacent point of intersection in the middle circle.
18. connect that middle-circle intersection with the inner-circle intersection along the same radius as the already connected outer-circle intersection.
19. complete the square by connecting the inner-circle intersection and outer-circle intersection with the intersection in the middle circle that the unfinished square opens toward.
20. repeat the last three instructions to complete the ring of eight squares.

 

The construction is complete; however, you might want to emphasize the figure by colouring or darkening its components.

 

3. With a sharp soft pencil (HB or softer) or three pencil crayons of different colours, or with a pen or three pens of different colours, darken

1. the outer circle in one colour; Nguyen used green.
2. the horizontal and vertical line-segments (as you look on the figure) in another colour; Nguyen’s was dark-blue.
3. the diagonal line-segments in a third colour; Nguyen used light-blue.

 

I stippled the squares and scumbled or hatched alternate rhombi to emphasize the three dimensional effect.

4. Check Nguyen’s post to compare your drawing with the original figure.

So did you do it? Did you get it right? What did you learn? I would love to know.

Send me your queries, your comments, your final drawings, your instructions for a new figure, and your reflections (both experiential and critical).

Follow @stefras

The Algorithm in the Code: Building an Inquiry Tool

A couple of days ago, I posted a Math Challenge posed by David Wees some weeks ago. The code — actualy, it is a pseudocode — emulated Euclid’s Algorithm of Coprimes and GCFs.

 

The Code in the Algorithm © 2012 David Wees | more info (via: yfrog)

 

First analysis

Glancing at the code reveals that, when a=0, b=b and, when b=0, a=a. This implies that one of the two values reaching zero is key to the code and the quantity of the other value when this happens is informative.

However, the ways a and b reach zero differ. a reaches zero at the code’s onset, while b does the same after the code runs through scenarios when b≠0.

Tabulating the difference between possible values of a and b within an arbitrary range of integers might illustrate how b=0 is reached. This process falls in the Planning and Implementation steps of David Coffey’s thinking-stage charts. Here is my table for mapping the “moves” of the code within the range of -9<a<9 and -9<b<9.

 

Table of Differences © 2012 Shawn Urban | more info (via: Stefras)
Click on image to get a printable copy.

 

Playing with b≠0

Notice that a>b below the a=b or 0 diagonal. So, for instance, the difference between a=6 and b=4 is 2, found in the bottom-left triangle of the table. In this triangle, according to the code, the difference a-b equals a. So, now a=2 and b=4.

Repeating the process using a=2 and b=4 produces a difference of 2, this time in the top-right triangle. The new difference b-a equals b. Now a=2 and b=2, which produces a difference b-a of 0. Since b-a = b, the code ends with b=0 and a=2.

 

Table of (6,4) © 2012 Shawn Urban | more info (via: Stefras)

 

Cases

There are six distinct cases where the code returns unique case results.

Case 1: a = b

When a=b, the code returns their common value. Why? As shown in the example above, the step after a=b is b=0 and the value of a is returned. This value is that when a=b.

Case 2: either a = 0 or b = 0

A starting value of a=0 returns b. A value of b=0, returns a. This is a rule built into the code. But what would happen if the rule were not followed?

Let’s take our b=0 and a=2 example beyond termination. Continuing the while-loop produces a difference a-b of 2, in the bottom-right triangle. This difference returns a=2 and b=0, exactly where we started.

What if a=0 and b=2? The difference b-a returns b=2 and a=0, another recursive repeat.

So, a=0 returns b and b=0 returns a. If a=b=0, zero is returned (in agreement with Case 1).

Case 3: a < 0, b < 0 or both < 0

When either a or b or both are negative, the code never resolves to termination (except when a=b, Case 4). In fact, the greater value iterates to infinity in steps of the lesser negative value.

Let us try a=3 and b=-2 (we could easily have tried a=-2 and b=3). The difference a-b returns a=5 and b=-2, which in turn returns a=7 and b=-2, then a=9 and b=-2, ad infinitum.

a=-3 and b=-2, on the other hand, returns (a=-3,b=1), (a=-3,b=4), (a=-3,b=7), again ad infinitum.

 

Table of (3,-2) © 2012 Shawn Urban | more info (via: Stefras)

 

Case 4: a = b < 0

Contrary to Case 3, when a=b<0, the common value of a and b is returned, in agreement with Case 1. Ignoring this, Case 3 is followed; however, there is no condition that rectifies the ambiguity of which direction, toward infinite a or infinite b, the map should follow.

Case 5: +a and +b share a common factor

When a and b share a set of common factors, the greatest of these factors is returned, as per the a=6 and b=4 example which returned 2, the greatest common factor of 6 and 4.

Case 6: +a and +b are coprime, or relatively prime

When a and b do not share a common factor, 1 is returned, since 1 is the only natural number that is a divisor of both.

Let’s map a=3 and b=8. As you can see from the table below, 1 is returned.

 

Table of (3,8) © 2012 Shawn Urban | more info (via: Stefras)

 

The analysis of cases weaves over and through David Coffey’s thinking-stage charts’ Analysis through Verification stages.

Interpretation and Pedagogy

I was introduced to the formal Extended Euclid’s Algorithm via induction within a discrete mathematics university course. It was taught to me as a means to learn modular mathematics, so not much emphasis was placed on explaining the Extended Algorithm nor the induction. In fact, given this challenge posed by David Wees, or perhaps more so the table derived from it, the manner in which I learned the Extended Algorithm was probably the worst possible.

David’s challenge and the table offer great entry tasks into the study of GFCs, coprimes, Euclid’s Algorithm and several branches of mathematics that build from them. Before the Algorithm is even named and formalized, students get to explore its mechanisms and formalize their own rules based on their mapping activities. Once they master the code and table, they can learn the corresponding Algorithm schema with emphasis on matching the items of the schema to the mapping on the table and the methods in the code. Then the Algorithm can be named and its uses illustrated.

For those students who do not know code, the teacher can interpret the pseudocode with them and offer scaffolding afterward. The pseudocode is probably easier to understand than an instruction list, if instead of treating it as code, the teacher treats it as an outline of process. Notice the subtle difference here between instruction (do this) and process (this is how this works).

The table doesn’t just determine GFCs and coprimes, it illustrates how greatest common factors and relatively prime, or coprime, numbers are calculated. It also illustrates why negative integers do not produce finite results, except where a=b, and why a=0 returns b and b=0 returns a.

One question that might remain is what the table and code return. In the case of positive integers, the returns are obviously GCFs or 1. Interpretation can determine whether the initial values are coprime or related by common factor. But what does the return of a when b=0 and the return of b when a=0 mean?

Quite simply the returns are the divisors of the numbers being analyzed. So, if one of those numbers is zero, it stands to reason that the other number is a viable divisor of zero. For instance, when b=0 and a=3, the return of 3 signifies that zero is divisible by three. Arithmetically, when a=b=0, infinity or undefinable should be returned, since conventionally no number “can” be divided by zero. This is the one flaw in this code and table.

In order for the constructed table to be a viable tool for learning Euclid’s Algorithm, it should be printed out or created with non-erasable ink and the mapping should be done with pencil and eraser. The table can be used several times then to build literacy, mastery and fluency of Euclid’s Algorithm.

Do you have any tasks that engage students in active learning of the outcomes, content, skills and concepts you are teaching?

Follow @stefras